Bulk Powder Storage Fly Ash Silo with CE Certificate
- Ref Price:
-
- Loading Port:
- Shanghai
- Payment Terms:
- TT OR LC
- Min Order Qty:
- 1 set
- Supply Capability:
- 100 set/month
OKorder Service Pledge
Quality Product, Order Online Tracking, Timely Delivery
OKorder Financial Service
Credit Rating, Credit Services, Credit Purchasing
You Might Also Like
Bulk Powder Storage Fly Ash Silo
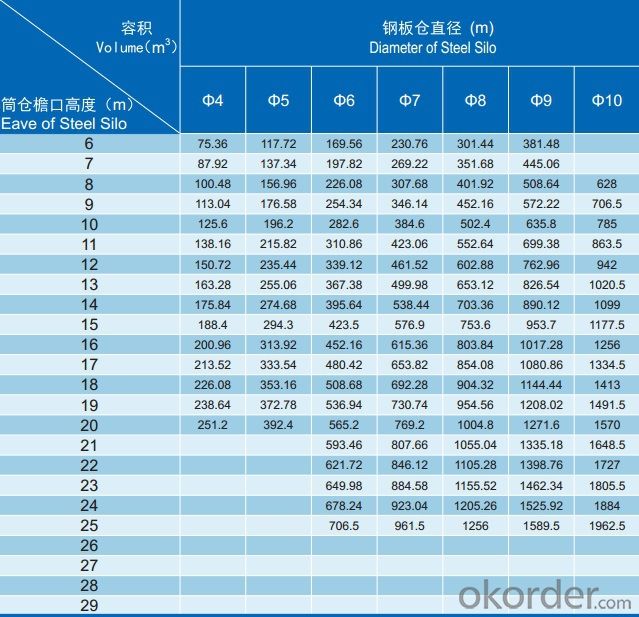
Specification of Bulk Powder Storage silo:
Process flow diagram of Bulk Powder Storage silo:
Advantages for Bulk Powder Storage Silo:
1. High strength: The spiral steel silo wall is reinforced by vertical stiffener and occluded by screw beam. It has great strength and good resistance to wind, earthquake and snow.
2. Good sealing function: Crimping and seaming of five-layer spiral steel plates ensures airproof, so our spiral steel silo can be used to store construction materials such as cement, gypsum, fly ash and slag, as well as liquids.
3. Small area occupancy: The smallest distance between spiral steel silos amounts to 600mm.
4. Short construction cycle: High-level automatic construction at site, Need only 5-6 days for a 1,000 tons spiral steel silo.
5. Long working life: 25-30 years, achieved by best combination of plates of different thickness for spiral steel silo body.
6. Nice appearance: The roof is subulate and is not easy to accumulate dust or water. The bin is shining and observable with silvery lines.
Pictures:
- Q:Hi..can someone answer this question step by step so i can understand how to do it?...it is decided to investigate the manufacture of a silo capable of of holding 10 000 m^3 of grain. The silo must be in the shape of a cylinder with a hemispherical roof. The grain is stored only in the cylindrical part, not in the roof (hemisphere section). The hemispherical roof costs twice as much per square metre to manufacture as the cylindrical part. What dimensions should the silo have in order to minimise the costs of manufacture?...the dimensions are 'r' (radius of cylinder) and 'h' (height of cylinder)...10 POINTS FOR BEST ANSWER...all answers are appreciated...thanks
- Let: V - grain volume a - cost to build 1 sq.m of cylindrical part Volume of cylindrical part is: pi*r^2*h = V So h = V / (pi*r^2) Total cost to build the silo is: Cost = pi*r^2*a (bottom of the silo) + 2*pi*r*h*a + 2*pi*r^2*2a (semi-spherical part cost twice) = = a*(5*pi*r^2 + 2*pi*r*h) = = a*(5*pi*r^2 + 2*pi*r*V / (pi*r^2)) = = a*(5*pi*r^2 + 2*V/r) You need to find minimum of the function dCost/dr = a*(10*pi*r - 2*V / r^2) = 0 r = (V/(5*pi)) ^ (1/3) = ... h = V / (pi*r^2) = ...
- Q:How are Missile silos constructed? how are they converted to homes? and how much would a missile silo cost for the public to buy? I need exact answers.. and if you could, send me a website link to where you got your knowledge about missile silos.. ^_^ Thank you for those who take my question seriously... (It's extra credit for science and I really need the extra credit...)
- sorry i didnt undertand jeje byebye amcfemale kisses
- Q:If Dave is standing next to a silo of cross-sectional radius r = 9 feet at the indicated position, his vision will be partially obstructed. Find the portion of the y-axis that Dave cannot see. (Hint: Let a be the x-coordinate of the point where line of sight #1 is tangent to the silo; compute the slope of the line using two points (the tangent point and (12, 0)). On the other hand, compute the slope of line of sight #1 by noting it is perpendicular to a radial line through the tangency point. Set these two calculations of the slope equal and solve for a. Enter your answer using interval notation. Round your answer to three decimal places.) Really confused on this question I dont even know where to start.
- You don't need any caluculs to do this problem. Draw the picture.... Unfortunately, the description here doesn't explain everything to solve the problem (where is the center of the silo in x, y space?) I am going to take a guess that it is at the origin. draw a line from Dave to the center of the silo. Draw a line from Dave to his line of sight, and continue it until it hits the y axis.... Draw the radius of the silo along the path from the center to the tangent point. The angle of obscured veiw is then t = acos (9/12) cos t = 3/4 sin t = (1-(3/4)^2) = sqrt (5)/ 4 tan t = sqrt 5 / 3 and the the section of the y axis that is obscured is [-12 tan t, 12 tan t] = [-4 sqrt 5 , 4 sqrt 5 ]
- Q:why is there always an odd number of silos in a grain elevator...one more on side than the other?
- why do you care?? why am i answering this q it is retarded
- Q:What is your reaction to this picture?
- Lmao, that's hilarious. At least, the part I think I understand is hilarious.. Help? o.o
- Q:a silo is to hold 1000 m^3 of corn. what dimensions will minimize the surface area?
- You didn't say what shape the silo is to be. For a given volume, the minimum possible surface area is always a sphere. However, silos are usually cylindrical, so that's what I'll assume here. The volume of the silo = pi r^2 h where r is its radius and h is its height. So, pi r^2 h = 1000 Its surface area A = pi r^2 + 2 pi r h h = 1000 / (pi r^2) So A = pi r^2 + 2 pi r [1000 / (pi r^2)] = pi r^2 + 2000/r The minimum surface area is found by setting dA/dr = 0 dA/dr = 2 pi r - 2000/(r^2) So 2 pi r - 2000/(r^2) = 0 2 pi r = 2000/(r^2) r^3 = 1000/pi r = (1000/pi)^(1/3) h = 1000/(pi r^2) = (1000/pi)(r^3)^(-2/3) = (1000/pi)(1000/pi)^(-2/3) = (1000/pi)^(1/3) = r So, the surface area of the silo is minimised if r = h = (1000/pi)^(1/3) = 6.83 metres (approx.)
- Q:Are Pakistan's nukes in some warehouse or are they in silos ready to fire?
- Who the hell really knowes.
- Q:A silo is to be constructed in the form of a cylinder surmounted by a hemisphere. The cost of construction per square foot surface area is twice as much for the hemisphere as for the cylinder. Determine the dimensions to be used if the volume is fixed (100m^3) and the cost is to be minimum.plz show stepsthanks in advance-lara
- Let V = volume of silo V = volume of hemisphere + volume of cylinder Volume of hemisphere = (2/3)(pi)r^3 Volume of cylinder = (pi)r^2h where r = radius of cylinder = radius of hemisphere h = height of the cylinder Since V = 100, 100 = (2/3)(pi)r^3 + pi(r^2)h and solving for h h = (100/(pi*r^2)) - (2r/3) S = Surface area of silo = surface area of hemisphere + surface area of cylinder Surface area of hemisphere = 2(pi)r^2 Surface area of cylinder = pi(r^2) + 2(pi)rh Therefore, S = 2(pi)r^2 + pi(r^2) + 2(pi)rh since h = (100/(pi*r^2)) - (2r/3) and substituting it in the above equation, S = 2(pi)r^2 + pi(r^2) + 2(pi)r[100/(pi*r^2)) - (2r/3)] Simplifying the above, S = 2(pi)r^2 + [(pi)r^2 + 200/r - 2(pi)r^2/3] S = 2(pi)r^2 + [(1/3)(pi)r^2 + 200/r] Since cost of hemisphere is twice that of the cylinder, then C = cost = 2*2(pi)r^2 + 1*[(1/3)(pi)r^2 + 200/r] C = 4(pi)r^2 + (1/3(pi)r^2 + 200/r C = (13/3)(pi)r^2 + 200/r Differentiating C with respec to r, (dC/dr) = (26/3)(pi)r - 200/r^2 and setting (dC/dr) = 0 and solving for r, (26/3)(pi)r - 200/r^2 = 0 Simplifying the above, 26(pi)r^3 = 600 Solving for r, r = 1.94 meters Now, that r is known, h can be determined by using the above derived formula of h = (100/(pi*r^2)) - (2r/3) Substituting r = 1.94. h = 7.16 meters Dimensions of the silo are: r = 1.94 m h = 7.16 m CHECK: First check: V = (2/3)(pi)(1.94)^3 + pi(1.94)^2(7.16) V = 15.3 + 84.7 = 100 m (this checks with the original condition of the problem that the volume of the silo is fixed at 100 m^3). Second check: Take the second derivative of the original function, i.e., (d^2C/d^2r) = 400/r^3 and since the second derivative is positive (greater than zero), then it confirms that the calculated dimensions for r and h will indeed yield the minimum cost.
- Q:It is the only way to keep Israel at bay, don't you think? Once mutually assured destruction is in place, maybe they will all behave and live in peace.
- Iran funds and arms Hezbolalh and Hamas, don't talk to me about peace.
- Q:when a earthquake hits the uk and your first thought is its a bomb are we really that terrified of the world i know iam. are we wrong to be scared should we live our life to the full or be scared
- Okay, wow. It's THEIR opinion. Just because MOST people aren't into the music you like DOESN'T mean it's dead. You can like it. They can like Tokio Hotel... I have a best friend who likes both. Really People should shut the **** up about their musical opinions. No one SAYS you have to hate this band because you like that one or whatever. REALLY PEOPLE! Music is a privilege NOT a given. What if the music you know and love wasn't there? So when you ask What is the world coming to someone likes Tokio Hotel Oh Emm Gee I haave to ***** about it Think about it. Next time Shut the **** up before you post.
1. Manufacturer Overview |
|
|---|---|
| Location | |
| Year Established | |
| Annual Output Value | |
| Main Markets | |
| Company Certifications | |
2. Manufacturer Certificates |
|
|---|---|
| a) Certification Name | |
| Range | |
| Reference | |
| Validity Period | |
3. Manufacturer Capability |
|
|---|---|
| a)Trade Capacity | |
| Nearest Port | |
| Export Percentage | |
| No.of Employees in Trade Department | |
| Language Spoken: | |
| b)Factory Information | |
| Factory Size: | |
| No. of Production Lines | |
| Contract Manufacturing | |
| Product Price Range | |
Send your message to us
Bulk Powder Storage Fly Ash Silo with CE Certificate
- Ref Price:
-
- Loading Port:
- Shanghai
- Payment Terms:
- TT OR LC
- Min Order Qty:
- 1 set
- Supply Capability:
- 100 set/month
OKorder Service Pledge
Quality Product, Order Online Tracking, Timely Delivery
OKorder Financial Service
Credit Rating, Credit Services, Credit Purchasing
Similar products
New products
Hot products
Hot Searches
